Algorithm: Truncated Wirtinger Flow (TWF)
Motivation
Under a stochastic noise model with independent samples, a first
impulse for solving 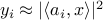 is to seek the maximum
likelihood estimate (MLE), namely,
is to seek the maximum
likelihood estimate (MLE), namely,
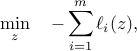
where 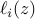 denotes the log-likelihood
of
denotes the log-likelihood
of  given
given 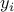 .
For instance, under the Poisson noise model
.
For instance, under the Poisson noise model 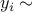 Poisson
Poisson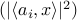 ,
, 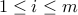 ,
one has
,
one has
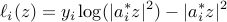
If we follow the Wirtinger flow 1 approach or other gradient descent paradigms, we would proceed as
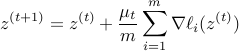
for some appropriate initial guess 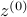 , where
, where 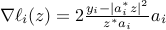 denotes the Wirtinger derivative (or ordinary gradient for the real case). Unfortunately, this approach does not work for real-valued case, since some of the gradient components
denotes the Wirtinger derivative (or ordinary gradient for the real case). Unfortunately, this approach does not work for real-valued case, since some of the gradient components 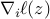 are abnormally large.
are abnormally large.
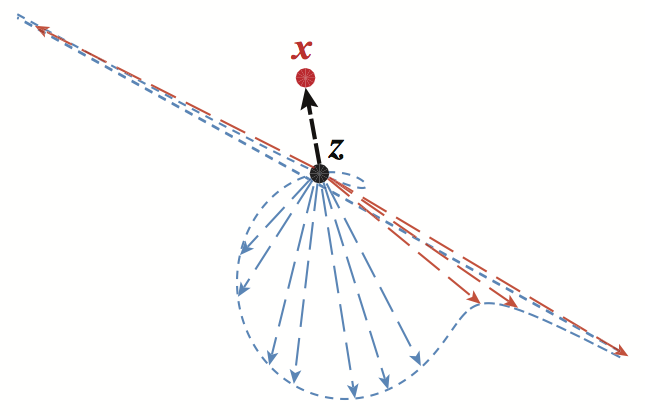 |
Figure 1: the locus of |
TWF methodology
TWF is a novel non-convex procedure that adopts a more subtle gradient flow, which proceeds in two stages:
(1) Truncated Spectral Initialization: compute an initial guess
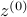 by means of a spectral method applied to a
subset of the observations
by means of a spectral method applied to a
subset of the observations 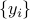 obeying
obeying
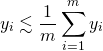
 |
Estimate after 50 truncated power iterations |
(2) Truncated Gradient Flow: for 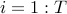 ,
,
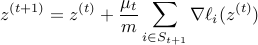
for some adaptive index set 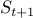 determined by
determined by 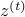 ; i.e. for any
; i.e. for any 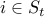 ,
,
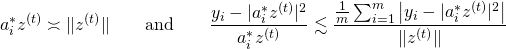
In words, the adaptive subset 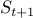 guarantees that both
guarantees that both 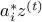 and
and 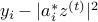 take typical values, and hence none of the gradient component
take typical values, and hence none of the gradient component 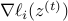 are abnormally large.
Here, the step size
are abnormally large.
Here, the step size 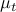 is either chosen to be a constant or determined by a backtracking line search.
is either chosen to be a constant or determined by a backtracking line search.
 |
Estimate after 50 TWF gradient iterations |
Detailed algorithmic procedure
By default, the step size and the truncation thresholds are set to be 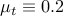 ,
, 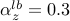 ,
, 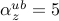 ,
, 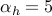 , and
, and 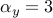 .
.
 |
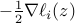 for all unit vectors
for all unit vectors 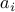 .
.